สมการริดเบิร์ก  (Rydberg  equation)

            จากความรู้เรื่องเส้นสเปกตรัม  ที่ว่าเกิดจากการที่อิเล็กตรอนที่อยู่ในระดับพลังงานสูง  คายพลังงานออกมาในรูปของคลื่นแม่เหล็กไฟฟ้า (photon) ทำให้ปรากฏเป็นเส้นสเปกตรัม  และมีผลให้ อิเล็กตรอน เปลี่ยนระดับพลังงานจากระดับพลังงานสูงลงมาอยู่ที่ระดับพลังงานซึ่งต่ำกว่า    

                สมการริดเบิร์กใช้ในการคำนวณหาความสัมพันธ์ระหว่างความยาวคลื่น ( ) ของเส้นสเปกตรัม  กับระดับพลังงาน  (n) ที่เปลี่ยนไปของอิเล็กตรอน    ฉะนั้นเมื่อทราบความยาวคลื่นของเส้นสเปกตรัม  จะ คำนวณได้ว่าอิเล็กตรอนเปลี่ยนระดับพลังงานจากระดับใดไปอยู่ที่ระดับใด  หรือในทางกลับกันถ้าทราบว่าอิเล็กตรอนเปลี่ยนระดับพลังงานจากระดับใดไประดับใด  ก็จะคำนวณหาความยาวคลื่นของเส้น สเปกตรัมได้การเปลี่ยนระดับพลังงานของอิเล็ตรอนของธาตุต่างชนิด  แม้จะเป็นช่วงพลังงานช่วงเดียวกันก็จะใช้พลังงานไม่เท่ากัน  ขึ้นอยู่กับจำนวนโปรตอน (เลขเชิงอะตอม , z ) ที่มีอยู่ในนิวเคลียสของ ธาตุนั้น ๆ  ธาตุที่มีโปรตอนมากจะใช้พลังงานในการเปลี่ยนระดับของอิเล็กตรอนมากกว่าธาตุที่มีจำนวนโปรตอนน้อย  สมการดังกล่าวเป็นดังนี้

 

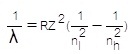
        λ   =  ความยาวคลื่น (M , เมตร)
                                R  =  ค่าคงที่ของริดเบิร์ก  =  1.097 x  10⁷  M^-1  หรือ 1/M   
                                Z  =  เลขเชิงอะตอมของธาตุ ; ถ้าเป็นธาตุ  H  ค่า Z=1
                              n_l  =  ระดับพลังงานต่ำของการเคลื่อนที่ของอิเล็กตรอน
                              n_h =  ระดับพลังงานสูงของการเคลื่อนที่ของอิเล็กตรอน 

ตัวอย่าง  เมื่ออิเล็กตรอนของไฮโดรเจนเคลื่อนที่จากระดับพลังงาน  n=4  ลงมาอยู่ที่ระดับพลังงาน  n = 3  อยากทราบว่าเส้นสเปกตรัมที่เกิดขึ้นมีความยาวคลื่นกี่  nm

             เมื่อทราบความยาวคลื่นย่อมคำนวณหาความถี่ของคลื่น (ν  , f )  ของสเปกตรัมนั้นได้  และทำให้คำนวณหาพลังงานของเส้นสเปกตรัมได้ด้วย  พลังงานดังกล่าวก็คือความแตกต่างของพลังงาน ระหว่างระดับพลังงานที่ทำให้เกิดเส้นสเปกตรัมนั้น     การหาค่าพลังงานจะทำได้  2 วิธีคือ  ใช้สมการของพลังค์  หรือใช้สมการของริดเบิร์กก็ได้   

แต่ถ้าใช้สมการริดเบิร์ก (บางครั้งเรียกว่าสมการของโบห์ร)  จะทำให้คำนวณหาความแตกต่างของพลังงานระหว่างระดับพลังงานต่าง ๆ ของแต่ละธาตุได้โดยตรง ดังนี้

 

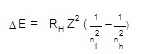
                                     ΔE  = พลังงานที่ต่างกันของระดับพลังงาน
                                     R_H  = ค่าคงที่ของริดเบิร์ก , Rydberg constant = 2.178 x 10^-18  J

                                       Z  =  จำนวนประจุในนิวเคลียส , nuclear charge  (จำนวนโปรตอนของแต่ละธาตุ)

ตัวอย่าง  เส้นสเปกตรัมสีแดงของไฮโดรเจนมีความยาวคลื่น  656  nm  มีพลังงานกี่จูล

วิธีที่ 2  คิดด้วยสมการของริดเบิร์ก  (เราต้องทราบว่าเส้นสเปกตรัมสีแดงของไฮโดรเจนเกิดจากการเปลี่ยนระดับ

แบบฝึกหัด 

1.  Calculate the E for the n = 4 to the n = 2 transition in hydrogen. (ans. 4.08375 x 10^-19 J  )
          (จงคำนวณหาความแตกต่างของพลังงานระหว่างระดับพลังงาน n=4  กับ  n=2 ของไฮโดรเจน)

                                                   (คลิ้ก ดูเฉลย)

2.  A hydrogen atom in its ground state absorbs light with a wavelength of 102.6 nm. Calculate the
         energy level of the resulting excited state (n = ?).
            (เมื่ออะตอมของไฮโดรเจนในภาวะปกติได้รับพลังงานจากคลื่นแสงซึ่งมีความยาวคลื่น  102.6  nm  จะมีผลให้
        อิเล็กตรอนเลื่อนขึ้นไปอยู่ที่ระดับพลังงานใด)

3.  Ionization energy is the energy required to completely remove an electron from and atom. This
             can be thought of as the transition between n = 1 and n = Calculate the energy needed to
             remove the electron from hydrogen in its ground state. 
              (พลังงานไอออไนเซชันคือพลังงานที่ใช้ในการทำให้อิเล็กตรอนหลุดออกไปจากอะตอมอย่างสมบูรณ์  คือ
              อิเล็กตรอนจาก n=1  ไปอยู่ที่  n = จงคำนวณหาพลังงานที่ใช้ในการทำให้อะตอมของไฮโดรเจนในภาวะ
              ปกติเกิดการเสียอิเล็กตรอนดังกล่าว) 

4.   What is the energy needed to remove the remaining electron from He⁺ in its ground state? Is it
              easier or harder to remove the electron from He⁺ than from H? 
               (จะต้องใช้พลังงานเท่าไรเพื่อทำให้    He⁺  เกิดการเสียอิเล็กตรอน  และพลังงานดังกล่าวจะมากกว่าหรือ
               น้อยกว่าการทำให้  H  เสียอิเล็กตรอน)

5.   What wavelength is predicted by the Rydberg equation for each of these electron transitions in
            the hydrogen atom?
              (จงใช้สมการริดเบิร์กคำนวณหาความยาวคลื่น  เมื่ออิเล็กตรอนของไฮโดรเจนเกิดการเคลื่อนย้ายตามที่
              กำหนดในแต่ละข้อ)

                a. n = 6 to n = 2  ; (ans. 410 nm)

b. n = 4 to n = 1 ; (ans. 97.3 nm)     

c. n = 7 to n = 3    ; (ans. 1005 nm)

d.  n = 4 to n = 2  ; (ans.486 nm)

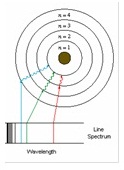
*Bohr applied this concept to the line spectra of elements. When elements are excited they emit

radiation at fixed wavelengths. He proposed that only certain energy levels are allowed

  within the structure of an atom. Electrons are allowed to move between these energy levels.

The light emitted by the elements is a measure of the energy gap between the two electronic states.  

        (เมื่อมีความเข้าใจเกี่ยวกับการค้นพบของโบห์รอย่างถูกต้อง  จะประยุกต์ใช้ในการอธิบายเส้นสเปกตรัมแต่ละเส้นของธาตุต่าง ๆ มีความยาวคลื่นคงที่  เป็นการบอกให้ทราบถึงความแตกต่างของพลังงาน             ระหว่างระดับพลังงานที่อิเล็กตรอนมีการเคลื่อนย้าย)
 

For the hydrogen atom,

                        ΔE =  R Z² (1/n²_l - 1/n²_{h )}
                         R = Rydberg constant = 2.178 x 10^-18  J

                         Z = nuclear charge ( 1 for H, 2 for He )

7.   A hydrogen atom in its ground state absorbs light with a wavelength of 102.6 nm. Calculate the
              energy level of the resulting excited state (n = ?).
               (เมื่ออิเล็กตรอนของไฮโดรเจนในสถานะพื้น  ได้รับพลังงานที่มีความยาวคลื่น  102.6 nm  อยากทราบว่า
               อิเล็กตรอนจะเลื่อนขึ้นไปอยู่ที่ระดับพลังงานใด)

*Ionization energy is the energy required to completely remove an electron from and atom. This can

be thought of as the transition between n = 1 and n = ∞  
(พลังงานไอออไนเซชัน  คือพลังงานที่ทำให้อิเล็กตรอนหลุดออกไปจากอะตอม  ในที่นี้ให้คิดว่าเริ่มจากอิเล็กตรอนอยู่ที่ระดะบพลังงาน n=1  ไปสิ้นสุดที่ n = ∞ )

8. Calculate the energy needed to remove the electron from hydrogen in its ground state.
            (จงคำนวณหาค่าพลังงานที่จะให้อะตอมของไฮโดรเจนจากสภาวะพื้นเกิดการเสียอิเล็กตรอน)

       This is the energy to remove an electron from the ground state of hydrogen. What wavelength of light  would work? Where is this on the EMS? 
        (พลังงานดังกล่าวมีความยาวคลื่นเท่าไรและอยู่บริเวณใดของแถบสเปกตรัม)

    9. What is the energy needed to remove the remaining electron from He⁺ in its ground state? Is it
            easier or harder to remove the electron from He⁺ than from H?
        (พลังงานที่จะทำให้อิเล็กตรอนของ  He⁺   หลุดออกไปมีค่าเท่าไร   ระหว่าง  He⁺ กับ  H  ใครเสียอิเล็กตรอน
             ง่ายกว่ากัน)

Size : 3.08 KBs Upload : 2015-04-01 20:55:33

ติชม กำลังแสดงหน้า 1/0 << 1 >>

ต้องการให้คะแนนบทความนี้่ ? 0 คะแนนโหวด สร้างโดย : K-Me สถานะ : ผู้ใช้ทั่วไป วิทยาศาสตร์