พันธะเคมี ตอนที่ 3 วัฎจักรบอน ฮาเบอร์
วัฏจักรบอร์น-ฮาเบอร์ (Born-Haber Cycle)
กระบวนการที่ประกอบด้วยขั้นตอนย่อย ๆ หลายขั้นตอน ทีมีทั้งคายความร้อนและดูดความร้อน เช่น
กระบวนการเกิดโซเดียมคลอไรด์
(NaCl)
โดยเริ่มต้นจากโลหะโซเดียมที่ยังเป็นของแข็ง (solid ,s) หรือ
Na(s) และเริ่มจากก๊าซคลอรีน (Cl2) หรือ Cl2(g) ซึ่งมีสมบัติเป็นโมเลกุล จะประกอบด้วยขั้นตอนย่อย
ๆ ดังนี้
1. โลหะโซเดียมซึ่งเป็นของแข็งได้รับความร้อนเกิดการหลอมเหลว ให้ความร้อนต่อไปจนเดือดและ
กลายเป็นไอ
ถ้าคิดรวมกันเป็นขั้นตอนเดียว คือจากของแข็งเป็นไอ (ก๊าซ) เพื่อไม่ให้มีขั้นตอนมาก
เกินไป จะเป็นการระเหิด เป็นกระบวนการดูดความร้อน ดังสมการ ;
Na(s) → Na(g)
; ΔH1
= +107 kJ/mol
2. อะตอมของ Na ในสถานะก๊าซ , Na(g)
ได้รับพลังงานจนเสียอิเล็กตรอน (พลังงานไอออไนเซชัน
อันดับ 1 , IE1) ขั้นตอนนี้
เป็นกระบวนการดูดความร้อน ดังสมการ
Na(g) → Na+(g) + e- ; ΔH2 = + 496
kJ/mol
3. โมเลกุลของก๊าซคลอรีน (Cl2) เกิดการแยกสลายออกเป็นอะตอมอิสระในสภาวะก๊าซ เป็นการสลาย
พันธะระหว่างอะตอมของคลอรีนในโมเลกุล ขั้นตอนนี้เป็นกระบวนการดูดความร้อน ดังสมการ
Cl2(g) → Cl(g)
; ΔH3 = +122 kJ/mol
4. อะตอมของ Cl ในสภาวะก๊าซรับอิเล็กตรอน กลายเป็นไอออนลบ กระบวนการนี้คายพลังงาน คือ
พลังงานอิเล็กตรอนอัฟฟินิตี , EA ดังสมการ
Cl(g) + e- → Cl-(g) ; ΔH4 = -349
kJ/mol
5. Na+(g) รวมตัวกับ Cl-(g) แล้วเปลี่ยนสถานะเป็นของแข็งคือผลึกของ
NaCl ขั้นตอนนี้คายพลังงาน
เรียกว่าพลังงานโครงร่างผลึก (lattice energy)
ดังสมการ
Na+(g) + Cl-(g) → NaCl(s)
; ΔH5 =
-787 kJ/mol
ถ้านำพลังงานที่เกี่ยวข้องกับขั้นตอนทั้ง 5 ขั้นตอนนี้มารวมกัน (นำเครื่องหมาย + หรือ – ของ
แต่ละค่ามาด้วย) ผลลัพท์ที่ได้เราเรียกว่า
พลังงานของปฏิกิริยา (ΔHf) ดังสมการ
ΔHf = ΔH1
+ ΔH2
+ ΔH3 + ΔH4 + ΔH5
= +107 kJ/mol + 122 kJ/mol + 496 kJ/mol
+(-349 kJ/mol) + (-787 kJ/mol)
=
- 411 kJ/mol
เขียนแสดงในรูปสมการรวมได้ดังนี้
Na(s) + Cl2(g) →
NaCl(s) ; ΔHf =
-411 kJ/mol
ในการคำนวณพลังงานของกระบวนการต่าง
ๆ ทำได้หลายวิธี ขึ้นอยู่กับความเข้าใจและความถนัดของแต่ละค น
แต่ต้องอยู่บนหลักการเดียวกันคือ
ต้องรู้ว่าพลังงานส่วนที่ดูดเข้าไปในแต่ละขั้นตอนรวมกันได้เท่าไร
รู้ว่าพลังงานส่วนที่คายออกมาในแต่ละขั้นตอนรวมกันได้เท่าไร นำพลังงาน
2 ส่วนนี้มาเปรียบเทียบกัน
ถ้าพลังงานที่ดูดเข้าไป มีมากกว่าที่คายออกมา กระบวนการนั้นเป็นกระบวนการดูดความร้อน (endothermic process)
; ΔH
ใช้เครื่องหมาย +
ถ้าพลังงานที่คายออกมา
มีมากกว่าที่ดูดเข้าไป
กระบวนการนั้นเป็นกระบวนการคายความร้อน (exothermic
process) ; ΔH ใช้เครื่องหมาย -
ในการเกิด NaCl จำนวน 1 โมล (58.5 กรัม) ดังตัวอย่างถ้านำความร้อนส่วนที่ดูดเข้าไปในแต่ละขั้นตอนมารวมกันจะได้ดังนี้
Na(s) → Na(g)
; ΔH1
= +107 kJ/mol
Na(g) → Na+(g) + e- ; ΔH2 =
+ 496 kJ/mol
Cl2(g) → Cl(g)
; ΔH3
= +122 kJ/mol
รวมพลังงานความร้อนที่ดูด ; = +107 + 496 + 122 = 725 kJ/mol
ในทำนองเดียวกันถ้านำความร้อนส่วนที่คายออกไปในแต่ละขั้นตอนมารวมกันจะได้ดังนี้
Cl(g) + e- → Cl-(g) ; ΔH4 = -349
kJ/mol
Na+(g)
+ Cl-(g) →
NaCl(s) ; ΔH5 =
-787 kJ/mol
รวมพลังงานความร้อนที่คาย ; ΔH2 -349 + (-787) = - 1136 kJ/mol
เมื่อเปรียบเทียบระหว่างพลังงานส่วนที่ดูดกับคายจะเห็นได้ว่า ส่วนที่คายมีมากกว่า ฉะนั้นกระบวนการนี้จึงเป็นแบบคายความร้อน ; ΔHf
= ΔH1 + ΔH2
= + 725 kJ/mol + ( -1136 kJ/mol )
= -411
kJ/mol
ปฏิกิริยานี้จะมีการคายพลังงานออกมา 411 kJ/mol เมื่อมี NaCl ที่เกิดขึ้น 1 โมล แต่ถ้ามี NaCl เกิดขึ้นมากหรือน้อยกว่านี้ การคายพลังงานก็จะแปรผันตรงกับจำนวนโมลของ NaCl ที่เกิดขึ้น
ถ้านำขั้นตอนต่าง ๆ
มาเขียนแสดงเป็นแผนผังตามลำดับ จะเรียกว่า Born Haber
Cycle หรือวัฏจักรของบอน ฮาร์เบอร์ ฉะนั้นวัฏจักรของบอน
ฮาร์เบอร์จึงเป็นแผนผังแสดงขั้นตอนของการการเกิดปฏิกิริยาและการเปลี่ยนแปลงพลังงานในแต่ละขั้น ดังนี้
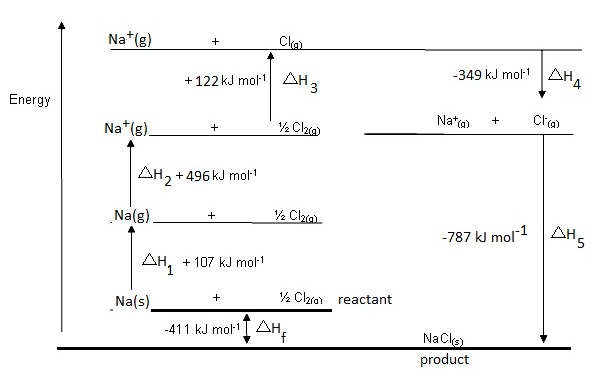
รูปแบบในการเขียนแสดงวัฏจักรของบอน
ฮาร์เบอร์
ไม่ได้กำหนดรูปแบบตายตัว
ความสำคัญอยู่ที่ความต่อเนื่องของขั้นตอน
และแสดงพลังงานที่เกี่ยวข้องให้ตรงกัน
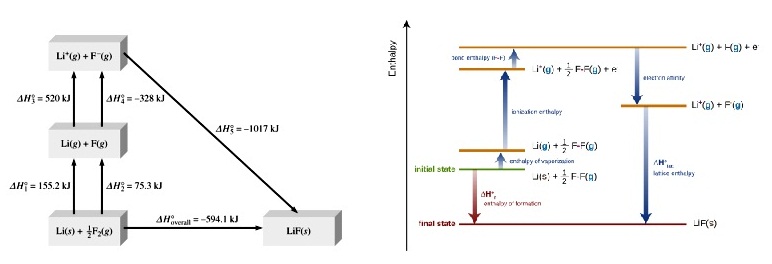
เช่น วัฏจักรของบอน ฮาร์เบอร์แสดงการเกิด LiF
สามารถเขียนได้หลายแบบ
เช่น
แบบฝึกหัด
1. Construct
a fully-labelled Born-Haber cycle for the formation of MgO and use the data
given below to calculate a value for the enthalpy of lattice formation of this
oxide.
(จงเขียนวัฏจักรของบอน ฮาร์เบอร์แบบเต็ม ของการเกิด MgO โดยใช้ข้อมูลที่กำหนดให้ต่อไปนี้)
Process H0 , kJ
mol–1
Mg(s) + O2(g) → MgO(s) –602
Mg(s) → Mg(g) +148
Mg(g) → Mg+(g) + e– +738
Mg+(g) → Mg2+(g) + e– +1451
O2(g) → 2O(g) +498
O(g) + e– → O–(g) –141
O–(g) +
e– → O2–(g) +798
2.
A Born–Haber cycle for the formation of calcium
sulphide is shown below. The cycle includes
enthalpy changes for all Steps except Step F. (The cycle is not
drawn to scale.)
(วัฏจักรของบอน
ฮาร์เบอร์แสดงการเกิดแคลเซียม
ซัลไฟด์
เป็นดังที่แสดงอยู่ด้านล่างนี้
แต่ละขั้นตอนได้
แสดงปริมาณความร้อนที่เปลี่ยนแปลงเอาไว้แล้ว ยกเว้นขั้นตอน F ไม่ได้แสดงเอาไว้)
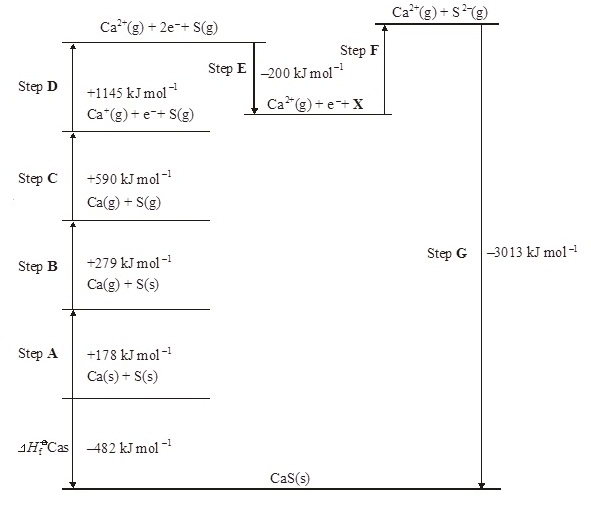
(a)
Give the full electronic arrangement of the ion S2–
(จงแสดงการจัดอิเล็กตรอนแบบเต็มของ S2-
......................................................................................................................................
(b) Identify the species X formed in
Step E.
(จงพิจารณาว่า X ในขั้นตอน E คืออะไร)
......................................................................................................................................
(c) Suggest why Step F is an endothermic process.
(จงให้ข้อเสนอแนะว่าเหตุใดขั้นตอน F จึงเป็นกระบวนการดูดความร้อน)
......................................................................................................................................
......................................................................................................................................
(d) Name the enthalpy change for each of the
following steps.
(จงจอกชื่อพลังงานที่เปลี่ยนแปลงในแต่ละขั้นตอน)
(i) Step B ...............................................................................................................
(ii) Step D ...............................................................................................................
(iii) Step F ................................................................................................................
(e) Explain why the enthalpy change for Step D is
larger than that for Step C.
(จงอธิบายว่าเหตุใดพลังงานที่เปลี่ยนแปลงในขั้นตอน D จึงมากกว่าขั้นตอน C )
(f) Use the data shown in the cycle to
calculate a value for the enthalpy change for Step F.
(จงคำนวณหาพลังงานที่ปลี่ยนแปลงในขั้นตอน F )
3.
The energy level diagram (Born-Haber cycle) for
caesium chloride is shown below.
(แผนผังแสดงแผนผังระดับพลังงานหรือ วัฎจักรของบอน
ฮาร์เบอร์ ของการเกิดแคลเซียมคลอไรด์เป็น
ดังต่อไปนี้)
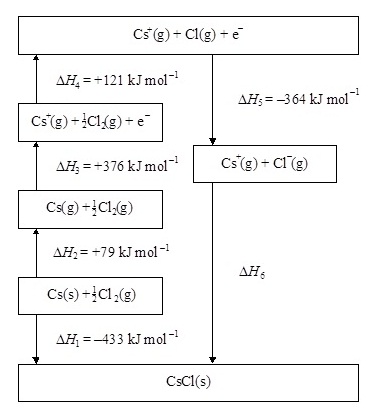
(a) Give the names of the enthalpy changes represented by ΔH1, ΔH2 and ΔH5.
(จงบอกชื่อพลังงานของ ΔH1, ΔH2 และ ΔH5.)
ΔH1 ...........................................................................................................................
ΔH2 ...........................................................................................................................
ΔH5 ...........................................................................................................................
(b)
Calculate the value of the lattice energy ΔH6.
(จงคำนวณหาพลังงานโครงร่างผลึก ΔH6)
(c) Explain why the
enthalpy change represented by ΔH3 has a lower magnitude for caesium than
for sodium.
(จงอธิบายว่าเหตุใดΔH3 ของซีเซียมจึงต่ำกว่าของโซเดียม)
.....................................................................................................................................
.....................................................................................................................................
.....................................................................................................................................
.....................................................................................................................................
4.
Figure 1 shows the energy level diagram (Born-Haber
cycle) for the formation of rubidium iodide from its elements.
(ภาพหมายเลข 1
แสดงแผนผังระดับพลังงานหรือวัฏจักรของ
บอน ฮาร์เบอร์ ของการเกิดสารประกอบรูบิเดียมไอโอไดด์ โดยเริ่มต้นจากขณะที่เป็นธาตุ)
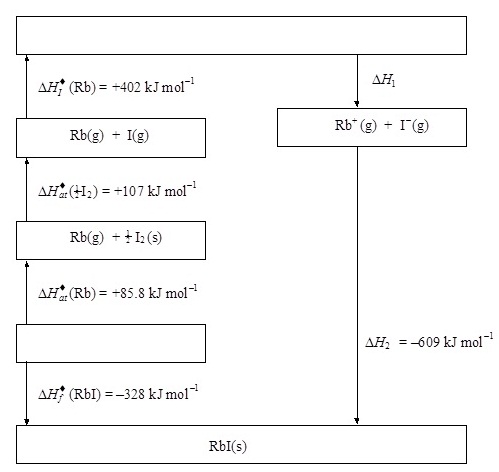
Figure 1
(i)
Complete the diagram giving the identities of the
missing species
(จงทำแผนผังให้สมบูรณ์ โดยเติมสิ่งเกิดขึ้นในช่องที่เว้นไว้)
(2)
(ii)
Give the names of the enthalpy changes represented by ΔH1 and ΔH2.
(จงบอกชื่อของพลังงาน ΔH1 และ ΔH2 )
ΔH1 ..................................................................................................................
ΔH2 ..................................................................................................................
(iii) Calculate the value of the enthalpy change represented
by ΔH1.
(จงคำนวณว่า ΔH1 มีค่าเท่าไร)
5. The following data relate to lithium chloride. Standard molar
enthalpy change of
solution is –37.0 kJ
mol–1.Lattice
enthalpy is –846 kJ mol–1.
(ข้อมูลต่อไปนี้เป็นของลิเทียมคลอไรด์ มีความร้อนมาตรฐานของการละลายต่อโมล = -37.0 kJ/mol และมี
พลังงานโครงร่างผลึก
= –846 kJ mol–1. )
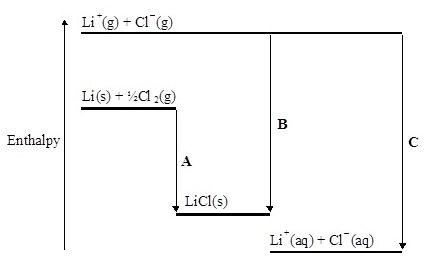
(i) Give the name of each of the changes A and B.
(จงบอกว่า A และ
B
เป็นการเปลี่ยนแปลงใด)
A...............................................
B...............................................
(ii) Calculate the value of the enthalpy change
represented by C and suggest the name(s) of the
enthalpy change(s).
(จงคำนวณหาพลังงานในขั้น C และบอกชื่อของพลังงานดังกล่าว)
6. (i) Draw
a fully-labelled Born–Haber cycle for the formation of solid barium chloride,
BaCl2, from its
elements10. Include state symbols for all species involved.
(จงเขียนแสดงวัฎจักรของบอน
ฮาร์เบอร์แบบเติม
ของการเกิดผลึกแบเรียมคลอไรด์ , BaCl2 โดยเริ่มต้นจาก
ขณะที่เป็นธาตุ จงระบุสถานะและสัญลักษณ์ของแต่ละขั้นตอนด้วย)
(ii) Use your Born–Haber cycle and the standard enthalpy data given below to
calculate a value for the electron affinity of chlorine.
(จงใช้วัฏจักรของบอน
ฮาร์เบอร์ที่เขียนขึ้นและค่าพลังงานต่อไปนี้คำนวณหาค่าอิเล็กตรอนอัฟฟินิตีของคลอรีน)
Enthalpy
of atomisation of barium +180
kJ mol–1
Enthalpy of atomisation of chlorine +122
kJ mol–1
Enthalpy of formation of barium chloride –859
kJ mol–1
First ionisation enthalpy of barium +503
kJ mol–1
Second ionisation enthalpy of barium +965
kJ mol–1
Lattice formation enthalpy of barium chloride –2056
kJ mol–1
รูปภาพที่เกี่ยวข้อง

Size : 2.11 KBs
Upload : 2012-11-25 09:14:40
|
|
ต้องการให้คะแนนบทความนี้่ ?
|
 
สถานะ : ผู้ใช้ทั่วไป
วิทยาศาสตร์
|
|
|